The first skill to be learned by the musician sometimes
involves tuning the instrument. For most of the band instruments
this requires a single adjustment to a reference pitch, and is
not really critical if the instrument is being played solo. The
multiple string and fretted instruments however, must have the
strings tuned to each other frequently. When tuning a fretted
instrument, each string can be tuned to the adjacent string, by
fretting one string appropriately and matching the open string
to the fretted string. Unfretted instruments are usually tuned
using a separate pitch reference for each string. Piano tuning
presents several problems and peculiarities. With more than 200
separate strings, this task is usually handled by a professional.
The process of setting the correct spacing between the notes
is known as setting the temperament. The equal tempered scale
used forms the basis for modern western music and will be described
in more depth. A further peculiarity in piano tuning is the practice
of stretching the upper and lower octaves. This refers to progressively
sharpening the notes of the upper octaves from a perfect equal
tempered scale. The reason for this has to do with what is known
as the inharmonicity of ringing strings. This phenomena will also
be described in detail. Understanding the equal tempered scale
and the rational for the stretching of the upper octaves in piano
tuning involves an understanding of something about both the physics
of sound, and the history of music.
The Phenomena of Sound and the Harmonic Series
Sound is the result of periodic fluctuations in air
pressure propagating through the atmosphere. When these pressure
fluctuations pass by the eardrum, we here sound. Differences
in the rate of fluctuation are perceived as differences in pitch.
Differences in the shape of the pressure wave forms are perceived
as differences in tone, or timbre. When these pressure fluctuations
strike a microphone, they are converted to electrical signals,
and an oscilloscope can then be used to observe how these pressure
wave forms vary as a function of time. A pure tone, such as from
a flute, will look like a nearly perfect sine wave. Most musical
wave forms are more complex than this. A tone produced by a reed
instrument, may appear to be shaped similar to a square wave.
You can imagine how the reed periodically opening and closing
would produce such a wave form. The wave form of a bowed violin
may resemble a saw tooth. This results from the way in which
the string is grabbed and released periodically by the bow. Each
of these tones may be of the same fundamental frequency, but the
ear and brain perceive distinct differences in timbre.
The harmonic series is an important concept in the
study of sound. It allows us to describe characteristics of sound
in terms of what our ears hear, rather than what our eyes see
when it is viewed on an oscilloscope. It also provides insight
into how different instruments produce the different sounds we
hear. The harmonic series consists of a set of frequencies which
are multiples of a fundamental. The frequency of any component
of the harmonic series can be figured using:
where N is the harmonic number, and fo is the frequency
of the fundamental. For example, if fo = 110 Hz and N = 1, then
the resultant frequency is 110 Hz, which is the fundamental.
If N = 2, the resultant frequency will be the second harmonic,
or 220 Hz. If N=3, the resultant frequency will be the third
harmonic, or 330 Hz. And so on. The fact that the first overtone
above the fundamental is called the second harmonic can lead to
confusion. Some references will refer to it as the first harmonic.
Therefore, whenever these terms are used, it is important to
realize whether it is the fundamental, or the first overtone,
which is being referred to as the first harmonic.
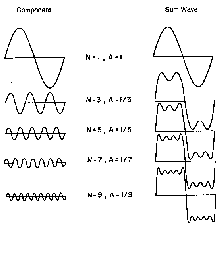
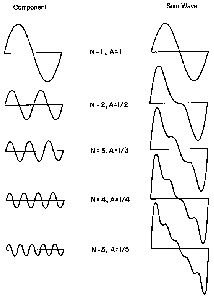
It can be shown, using a branch of mathematics known
as Fourier analysis, that any periodic wave form is composed of
a summation of frequencies from the harmonic series. If only
the odd harmonics, that is odd values of N, are summed in the
proper proportions, the resulting wave form will resemble a square
wave. Likewise, a saw tooth wave form can be generated by summing
both odd and even harmonics in the proper proportions:


It is possible to create any periodic wave form by
a summation of weighted elements of the harmonic series. This
has direct application in music synthesis. It is also useful
to decompose a sound wave form into its component harmonics.
A spectrum analyzer is used for this purpose. The spectrum analyzer
samples the sound wave forms, and displays a graph of magnitude
as a function of frequency. When the spectrum of a periodic wave
form is viewed on such an instrument, there will appear a peak
at the fundamental, and a series of peaks at each harmonic present
in the wave form:
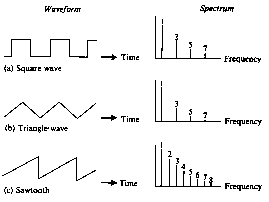
Real sound wave forms however are more complex. They
change with time or may even have overtones which are not perfect
multiples of the fundamental. It is interesting to note that
wave forms with mirror symmetry are composed of odd harmonics
only. This is why distortion which results from the clipping
of the top of the wave form, such as when over driving an amplifier,
is sometimes referred to as "odd harmonic" distortion.
The ability to describe a wave form in terms of its frequency
components is also useful because this resembles the way the ear
hears. The function of the ear is to detect the relative strength
of each of these frequencies, while the brain interprets this
information as both pitch and timbre. The difference in sound
we perceive between a saxophone, a bowed violin string or a flute
can be explained in terms of the harmonic content of the sound
wave forms.
Another important phenomena encountered in the study
of sound is the beat. When two notes, which are slightly different
in pitch, are played simultaneously, a resultant modulation can
be perceived as a slow periodic change in volume or timbre. This
is known as the beat. This beat rate slows as the pitches are
brought closer and stops when they are exactly matched. The cause
of this is that as both notes are combined by the eardrum or microphone,
the frequency difference results in a steady shift in the phases
of the two notes. As the phase difference shifts from constructive
to destructive interference, a slight difference in volume and
timbre is perceived.
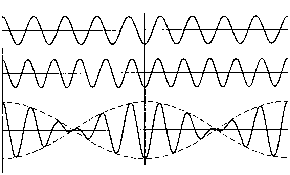
The rate at which this occurs is equal to the difference
in frequency. If a 440 Hz tone and a 441 Hz tone are sounded
together, a beat rate of 1 Hz will be heard. By sounding two
notes close in pitch, and adjusting one so that the beat rate
slows until it is stopped, a process known a zero beating, two
notes can be tuned extremely accurately. Even someone who would
consider themselves tone deaf can do this, if they know what
to listen for.
Beats are also perceived between a tone and its
natural harmonics. For example if a tone of 440 Hz is sounded
with a tone of 660 Hz ( (3/2)440, or a natural fifth) the resulting
tone will be beatless. If however, the 660 Hz tone is shifted
to 659.2551 Hz, a beat rate of .745 Hz will be heard. This corresponds
to 3 beats every 4 seconds, or a metronome setting of 45 beats
per minute. If you play A5 and E5 together on a properly tuned
piano this is exactly what will happen. This is a result of the
equal temperament used in modern music.
The Physics of Ringing Strings
Sounds containing periodic wave forms are produced
in many ways. Initially primitive music was based on rhythm.
An object with elastic properties is struck, and it vibrates,
radiating pressure fluctuations which rapidly decay. Methods
were discovered of generating sustained tones. One involved the
plucking of stretched strings. Another the resonating of columns
of air in tubes. The air column could be resonated by blowing
across the end, like the flute, or buzzing ones lips in the end,
like the horn. With the realization that several pitches could
be produced by varying ones lip technique, the natural harmonic
was discovered.
A stretched string, plucked carefully, will ring
with pure tone. Due to it's elastic properties, the string oscillates
back and forth between two gentle curves. The condition is known
as the fundamental mode of oscillation. If the length is cut
in half, say by pressing the string down to a fret, it will ring
in a similar manner at twice the frequency, or an interval of
one octave above the fundamental. This property of a stretched
string was first identified by the Greeks.
A string can be induced to ring in modes other than
the fundamental. By gently touching the string at its midpoint
while plucking it, a mode is induced with two gentle curves, crossing
in the middle. The point at which the curves cross is called
a node, and each section between nodes rings exactly as though
it were a string of that length. In this case the pitch produced
is 2 times the fundamental pitch which is an interval of one
octave above the fundamental. By touching the string at the 1/3
point (above the 7th fret), a mode is induced with two nodes and
three ringing sections. The pitch produced is 3 times the fundamental,
which is an interval of one octave plus a major fifth. By touching
the string at the 1/4 point (above the 5th fret), a mode is induced
with 3 nodes and four ringing lengths. The pitch produced is
4 times the fundamental, an interval of two octaves. By touching
the string at the 1/5 point(above a spot between the 3rd and 4th
frets), a mode is induced with 4 nodes and 5 ringing lengths.
The pitch produced is 5 times the fundamental, an interval of
two octaves plus a third. By touching the string at the 1/6 point,
a mode is induced with 5 nodes and 6 ringing sections. The pitch
produced is 6 times the fundamental, which is an interval of two
octaves and a fifth. This process continues:
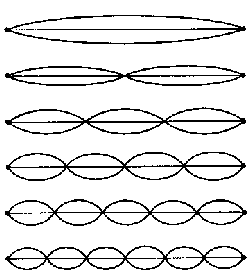
When a string is plucked, it produces the pitch of
the fundamental, as well as a series of overtones harmonically
related. This is due to the fact that the string is excited in
several modes of oscillation. As the string rings, the higher
modes will decay, leaving predominately the fundamental mode.
This combination of decaying overtones results in the distinctive
sound of a ringing string. Careful measurements will show that
the overtones of the string are not necessarily perfect harmonics.
To differentiate between the ideal harmonics and the pitches
actually produced, the actual overtones produced by the string
are called partials. Although the partials are very close to
the ideal harmonic series, they can differ. This effect becomes
important in the art of piano tuning.
The Evolution of the Equal Tempered Scale
Early musical scales and harmonies were based on
intervals from the natural harmonic series. The natural third
and fifth intervals can be combined to form pentatonic scales
(with five intervals dividing the octave, such as the pentatonic
blues scale). With additional natural third and fifth intervals
diatonic scales can be formed. A diatonic scale divides the octave
into eight intervals. These eight intervals consist of 5 large
steps and 2 small steps. Each of these large steps is referred
to as a whole tone interval, and each small step is referred to
as a semi-tone interval. A semi-tone interval is half a whole
tone interval. By rearranging the pattern of whole tones and
semi-tones, scales can be formed with different tonal characteristics.
The major and minor scales are examples of diatonic scales. By
splitting each whole tone, a twelve tone chromatic scale can be
formed. A scale developed like this from pure harmonic intervals
is known as a just toned scale. Modern musical terminology developed
from the early use of these types of diatonic scales. The interval
from the root note to the eighth note of the scale is referred
to as an octave. The interval from the root note to the fifth
note in a major scale is referred to as a major fifth. The interval
from the root note to the third note in a major scale is referred
to as a major third. It works out that the fifth interval is
obtained by multiplying by 3/2 (or 2/3 to descend a fifth), and
the third interval is obtained by multiplying by 5/4. So, the
numerical ratio of frequencies of the fifth, has nothing to do
with 5, and the ratio of frequencies of the third, has nothing
to do with 3.
A twelve tone chromatic scale can also be developed
as a natural consequence of the cycle of fifths. The Chinese
discovered the cycle of fifths more than 5000 years ago. This
is how it works: Begin with a root note, and play the note a
fifth above it. Then you play the note an interval of fifth above
this note. If this process is repeated a total of twelve times,
you will end up with a note very close to the root note you started
with, only seven octaves higher. If each of these notes is translated
down by octaves, a scale can be formed dividing the octave into
twelve intervals.
An interesting thing happens if you actually play
a cycle of fifths using only intervals which are perfect natural
fifths, that is where each interval is exactly (3/2)fo. If you
start with fo = A0 = 27.5 Hz, then the twelfth interval will result
in f = 3568.02 Hz. If on the other hand, you start at A0, and
play perfect octaves up to A7, you will get f = 3520 Hz. This
can be quickly verified on a hand calculator; try it. This difference
in pitch between the twelfth note of a natural fifth series, and
a natural octave series of 48.02 Hz results in a pitch error of
24 cents, almost a quarter of a semi tone. If on the other hand,
you play a cycle of fifths using intervals which are each slightly
flat by just the right amount, when you reach the twelfth interval,
you will end with f =3520 Hz! If each fifth in the series is
flattened by the same amount and the adjustment distributed evenly
throughout the cycle, it works out that each fifth should be played
flat by 2 cents. When the resulting twelve notes are all shifted,
by octaves, into ascending order, the result is an equal tempered
chromatic scale. The spacing between the notes of this scale
will have intervals which are all equal.
The advantage of this equal tempered scale over a
just toned scale may not be apparent at first. In fact, harmonies
played on a just tone scale may sound purer because of the total
absence of any beats produced by the natural intervals. But it
becomes clear when harmonies are shifted to other keys. The
intervals between the notes of a just toned scale are not constant.
When the patterns of intervals making up a chord are shifted
in key in a just toned scale, the intervals within the chord are
shifted very slightly, resulting in some chords with beats that
can clash quite badly. In an equal tempered scale, chords can
be shifted at will without harmful effect.
Two developments occurred in music technology which
necessitated changes from the just toned temperament. With the
development of the fretted instruments, a problem occurs when
setting the frets for just tuning, that octaves played across
two strings around the neck would produce impure octaves. Likewise,
an organ set to a just tuning scale would reveal chords with unpleasant
properties. A compromise to this situation was the development
of the mean toned scale. In this system several of the intervals
were adjusted to increase the number of usable keys. With the
evolution of composition technique in the 18th century increasing
the use of harmonic modulation a change was advocated to the equal
tempered scale. Among these advocates was J. S. Bach who published
two entire works entitled; "The Well-tempered Clavier".
Each of these works contain 24 fugues written in each of twelve
major and twelve minor keys and demonstrated that using an equal
tempered scale, music could be written in, and shifted to any
key.
Piano Tuning
The initial task of a piano tuner is known as setting
the temperament, that is, to tune a section in the middle of the
keyboard to an equal tuned temperament. Once this is done, the
rest of the strings may be set by tuning octave intervals up and
down the keyboard. The trick then, is in adjusting the spacing
between notes over a two octave range, starting with a single
C tuning fork. One might suspect this could only be done if one
had perfect sense of pitch, but this is not necessary. There
are systematic methods of setting the temperament which depend
on setting intervals to natural harmonics, and then adjusting
them sharp or flat by listening to, and adjusting for a specific
beat rate. Beat rates can be adjusted to the speed of a metronome,
and measured quite accurately. A tuner, armed with a good sense
of time, and an ear that knows what to listen for, can very accurately
set the temperament from a single pitch reference.
The are many systems of temperament setting, The
Fischer method is not generally used, but has an advantage of
simplicity. First, a strip of felt is looped between each group
of three strings over a two octave interval to damp out the outside
strings in each group and allow only the middle string to ring
when struck. Middle C is tuned directly to a fork. Then the
octaves above and below are tuned against middle C until the intervals
sound beatless. The next step is to actually set the temperament.
When finished, the two octaves between the upper and lower C
already tuned, will be set to equal temperament. The interval
from the C to G in the lower octave is tuned to a beatless natural
fifth, then flattened slightly to a beat rate of .7 beats per
second forming an equal tempered fifth. Then the G in the second
octave is tuned beatlessly to the lower G. Next, the D in the
second octave is tuned to the lower G , 2 cents flat of a natural
fifth, with a slightly faster beat rate. This procedure continues
on up through the cycle of fifths until both octaves are tuned.
The catch is, that the beat rate corresponding to 2 cents on
the highest fifth interval used is 1.4 beats per second, rather
than .7. As each interval is adjusted flat, the beat rate must
steadily increase from .7 to 1.4 beats as the interval moves up
the keyboard. Using a metronome, one can measure the beat rate
accurately and develop a good sense of timing to be able to make
this adjustment smoothly. The final fifth of the series ends
back on C, and must end up with the proper beat rate. Once the
two temperament octaves are completed, the damper strip is removed
and the outside strings in each group are tuned beatlessly to
the middle string. This is known as tuning the unisons. Wedges
are used to damp each edge string while tuning the other. Finally
the remaining strings are tuned to the temperament octaves using
beatless octave intervals up and down the keyboard.
When one measures a piano that has been tuned by
a skilled tuner, something interesting will be discovered. The
middle of the piano will be close to perfect, while somewhere
about the second octave above middle C, the notes will gradually
become sharper, until at the high C this sharpening may be as
high as 20 to 30 cents! Also there will be some flattening of
the notes in the lower octaves. Shown is a plot of actual measurements
of a piano tuned by a skilled tuner, along with a curve resulting
from the average of many such measurements:
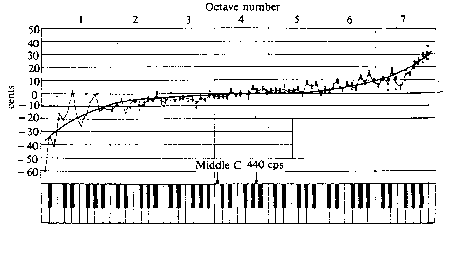
This affect is known as the "stretching"
of the upper and lower octaves. It is due to the fact that a
string does not necessarily vibrate at perfect natural harmonics.
The harmonics of a vibrating string tend to be sharp of the natural
harmonic series. This becomes more pronounced as the string is
made shorter or thicker. When the tuner is tuning octave intervals
up the keyboard, they tune for the best sound, compromising the
beat between the string fundamentals and the beat between the
octave partial of the lower note to the fundamental of the upper.
This produces a slightly sharp octave interval between the two
strings. This slight adjust accumulates towards the high and
low end. If a piano is tuned to a perfect scale top to bottom,
the beats produced between partials of the high strings clash.
A piano tuned with the upper and lower octaves stretched just
sounds better.
The shape and degree of the stretch is dependent
on the string configuration of the instrument. Pianos with longer
bass string sections require less stretch in the lower end. In
principal then, a piano could be fairly well tuned using a tuning
indicator device, such as a Precision Strobe Tuner, and adjusting
the device calibration accordingly across the keyboard. A further
refinement of this method might be to develop and use different
tuning curves for pianos of different construction. A simplification
of the above method would be to tune the piano correctly up the
keyboard to about E5. From this point up, progressively sharpen
each note about .5 cent ending at C7 sharp about 30 cents. This
two line curve fit can be readily set using a chromatic tuning
indicator device and seems to result in a reasonably well sounding
tuning. This is probably a good starting point for the beginning
and amateur tuner. There are algorithms and software available
which will calculate a temperament for a given piano based on
inharmonicity measurements. There are also people who will say
this can be done properly only by human ear. Unfortunately,
this is a skill that seems to be falling into decline. Perhaps
the best method for the amateur tuner of finding the best temperament
of a given piano is to locate a skilled tuner who tunes by ear
and have them tune the piano. The stretch could then be measured
and recorded for future use. Of course, a student with patience
and perseverance can learn to tune a piano properly using a single
pitch reference and their ears. It is said this is a skill that
can take years to develop. If the number of skilled piano technicians
continues to decline, it is a skill that could become more and
more valuable.
The goal of musical instrument adjustment and tuning
is an instrument that sounds good. The qualitative definition
of what sounds good has been being developed by musicians and
instrument makers for thousands of years. Modern technology has
provided the tools to make very accurate quantitative measurements
of these qualities. But these tools are only tuning aids, alone
they do not guarantee the goal of adjusting an instrument so that
it sounds good. As we have seen, a piano tuned perfectly to an
equal tempered chromatic scale will not sound as good as one that
has been stretched somewhat in the upper and lower octaves. However,
when these tools are used along with a bit of judgment based on
knowledge of music, good results can be obtained.
The octave is divided into twelve intervals to form
the chromatic scale. Each of these intervals is further divided
into 100 cents. Cents are used to describe small differences
in pitch in terms of percentage of a semi tone.
Intervals of pitch are described in terms of the
ratios of the frequencies, not absolute difference in frequencies.
An octave interval is always twice, or half the frequency, of
the first note. In the equal tempered scale, the twelve intervals
are spread evenly between the octaves. If the ratio of each semi-tone
is the inverse of the twelfth root of two (1.059463), this condition
will be met. The frequency of each note in the scale can be figured
by multiplying each successive note by this number to get the
next. The frequency of any note can also be figured from:
f(N) = 27.5*2^(N/12)
where N is an index into the chromatic scale notes
starting with 0 for A0, the lowest note on the keyboard. N increases
by 1 for each note on the keyboard. Note that the actual key
on the keyboard is N + 1. Table 1 shows the index and corresponding
frequencies for all of the keyboard notes based on A4 = 440 Hz.
To find the frequency of a note 12 cents sharp from A4, a value
of n = 48.12 would be used. Sometimes it is useful to convert
a frequency into N, solving for N:
N(f) = (12/ln(2))*ln(f/27.5)
This formula can be used to determine the note corresponding
to a given frequency. Once N is figured, the integer value closest
to it can be looked up in the following table. This equation
also tells you the cents error from the corresponding note by
taking the difference from it to the closest integer and multiplying
by 100.
Appendix B. Further Reading:
The Science of Sound
The Acoustical Foundations of Music
Piano Servicing Tuning & Rebuilding
PIANO TUNING, A Simple and Accurate Method for Amateurs
THE SEVENTH DRAGON: The Riddle of Equal Temperament
"The Endangered Piano Technician"
Thomas D. Rossing (1982), Addison-Wesley Publishing
John Backus (1977), W W Norton and Company
Arthur A. Reblitz (1993), The Vestal Press
J. Cree Fischer (1907)
Anita T. Sullivan (1985), Metamorphous Press.
Essay, James Boyk, Scientific American December 1995